ELEC 320
Prof. Rich Kozick
Notes for Homework 10
Problem:
Prove that for a continuous-time system that
is linear and time-invariant,
the zero-state response (ZSR) of the system to a sinusoidal input
is a sine wave with the same frequency as the input wave,
but a different amplitude and phase shift.
Also, find an expression for the frequency response
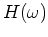 of the system in terms of the impulse response
of the system in terms of the impulse response 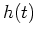 .
.
Use the following approach.
- Please explain why it is true that the ZSR of any
linear, time-invariant (LTI) system is completely described by
the impulse response
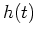 of the system.
(Are there any LTI systems for which this is not true?)
If the impulse response
of the system.
(Are there any LTI systems for which this is not true?)
If the impulse response 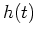 is known, then the system
output
is known, then the system
output 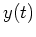 due to any input
due to any input 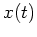 is given by
is given by
- Now consider a particular input
 that is applied to a LTI system with impulse response
that is applied to a LTI system with impulse response 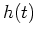 .
Put this
.
Put this 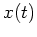 into the convolution integral,
and look at the resulting
into the convolution integral,
and look at the resulting 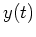 .
You should be able to recognize that
.
You should be able to recognize that 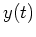 is a sine
wave with the same frequency
is a sine
wave with the same frequency 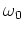 , but with
a different amplitude and phase shift.
The trigonometric identities at the bottom of the page
will be helpful.
, but with
a different amplitude and phase shift.
The trigonometric identities at the bottom of the page
will be helpful.
- In terms of the frequency response of the system
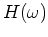 , recall that we expect that the system output
has the form
, recall that we expect that the system output
has the form
Use your result from item 2 to relate the frequency response
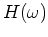 of the system to the impulse response
of the system to the impulse response
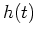 .
This provides a mathematical connection between the
frequency domain and time domain descriptions of a system.
.
This provides a mathematical connection between the
frequency domain and time domain descriptions of a system.
- You now understand the very important result
that a sine wave input to a LTI system produces a
sine wave output with the same frequency but different
amplitude and phase shift!
Here are some useful identities:
where
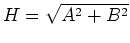 and
and
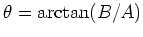 .
.