ELEC 101
Prof. Rich Kozick
Spring, 1998
Homework Assignment 10
Date Assigned: Monday, March 23, 1998
Date Due: Friday, March 27 and Monday, March 30, 1998
Reading:
Relevant reading in the Bobrow text to supplement the class notes
are Sections 4.1, 4.2, 4.3, and 5.1.
Problems:
Please submit solutions to the following problems on
Friday, March 27.
- 1.
- For each sine wave, find the phasor representation
(in polar form), and sketch the phasor in the complex plane.
- (a)
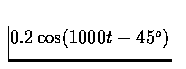
- (b)
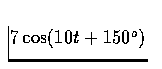
- 2.
- For each phasor, express the corresponding sine wave as
a time function, and sketch the sine wave versus time.
Assume
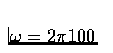 .
.
- (a)
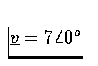
- (b)
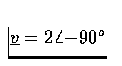
- 3.
- Find the magnitude of each complex number below.
- (a)
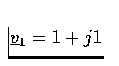
- (b)
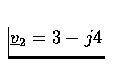
- (c)
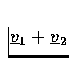
- (d)
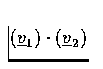
[CONTINUED ON BACK OF PAGE]
Please submit solutions to the following problems on
Monday, March 30.
- 1.
- A circuit and its phasor/impedance equivalent are
shown below.
Determine the current i(t), and sketch i(t) versus t.
Indicate the sine wave amplitude, frequency, and phase in the sketch.
Note that
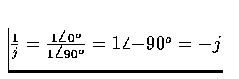 .
.
CIRCUIT OMITTED IN HTML DOCUMENT -- SEE PAPER COPY
- 2.
- Classify each circuit below as one of the following types
of filter: low-pass, high-pass, or band-pass.
You can do this either by thinking about how each circuit operates
as
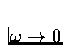 and
and 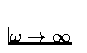 ,or you can analyze the circuits as voltage dividers with
impedances and study the resulting equations.
,or you can analyze the circuits as voltage dividers with
impedances and study the resulting equations.
CIRCUIT OMITTED IN HTML DOCUMENT -- SEE PAPER COPY
Kozick Rich
3/22/1998
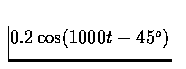
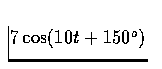
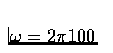 .
.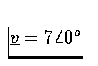
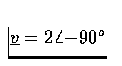
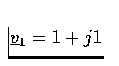
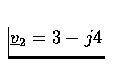
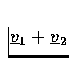
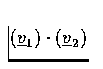
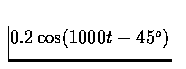
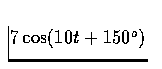
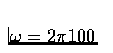 .
.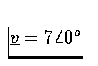
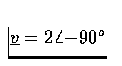
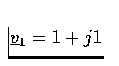
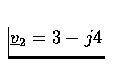
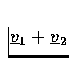
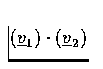
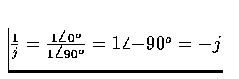 .
.
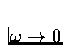 and
and 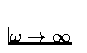 ,or you can analyze the circuits as voltage dividers with
impedances and study the resulting equations.
,or you can analyze the circuits as voltage dividers with
impedances and study the resulting equations.