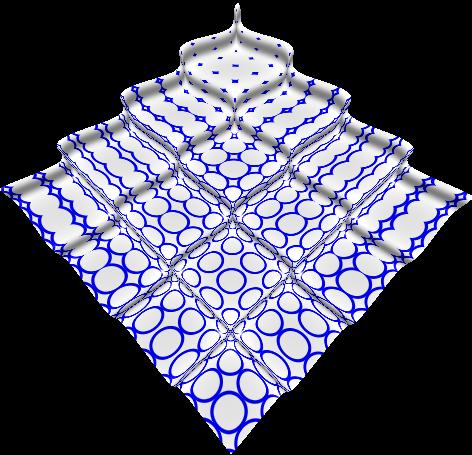
figure: A ring pattern on two surfaces.  The size of a given ring is modulated by the magnitude
of the partial derivatives with respect to the surface parameters.  To learn more about the
windmill or the qubert surfaces, follow the links.
 

    The assignment was to make a procedural shader.  I decided to implement
mine through the recently presented Ashli Gl Viewer for the ATI 9700 card.
This Renderman implementation offered advantages over other methods, yet
it's incompleteness caused a lot of needless delay.  On this web page, I will
discuss first, my shaders, and then my experiences with the Ashli Viewer.

Shader 1: rings, and rings-qub

    These shaders started with a ring shader on Steve May's RmanNotes
website.  I wanted the rings on the surface to be modified according to local
surface properties.
    The first part is the creation of the rings themselves.  The texture
coordinates s and t are known at a point.  There are two radii to the rings,
the inside and outside.  We pick regularly spaced (in s and t) points to be the
centers of the rings, and then color the surface blue if the (s, t) lie within the
two radii of one such center.
    The second parts of the two shaders make the assumption of either of
the two surfaces above.  I found that the Du, Dv operations are not
supported in the Ashli Viewer.  In that I know the parametric functions that
are the surfaces, I can easily compute the derivatives with respect to s,t at a
particular texture (s,t) point.  I then use this number to modulate the radius
for the rings.  Thus, the rings get larger as the derivatives get larger.

Shader 2: fallingwater

    This shader simulates water flowing radially over a surface, and also
modifies the flow with respect to local surface geometry.  I start by putting
sticky noise on the surface--sticky meaning noise that is dependent on the
local texture coordinates, so that movement of the object doesn't change the
pattern.  The surface looks made of tiny stones here.  Next, I use (s,t) to
determine how far from a corner of the surface (s,t = -5 in my case) is the
current point.  If this distance is smaller than a time-proportional number, I
do several things.  First I add blue to the color at that point and use time-
dependent noise to modify the normal for specular and diffuse calculations.
Second, if the point is within a region along the current border of the water,
noise is added to the color to make it look like the water is being broden up
by the small stones.
    An additional computation based on local geometry is done to the original
distance for better look and realism.  The differentials of the surface with
respect to the s and t surface parameters in the z (down) direction are
computed.  A number that is proportional to the downward orientation of
the surface at a point, or the magnitude of these partials, is added to the
original distance.  Thus if the point is in a downward sloping area, the
distance computed is big enough to render the point in the water when it
otherwise might not be.

Overall:

    Looking over the web, it is obvious that some people really dig
procedural shaders and modeling.  It is high on my list of hobbies if I ever
have time.  For this assignment, I would like to have had more time on the
cool creative side, but it would hard to compete with some of the obsessed
inspired people out there.
    The Ashli Viewer is not a product, so I should not have actually tried to
to use it without the source code at my disposal.  Many standard
Renderman functions are missing that would have proved useful.  As well,
the delay caused by incorrect implementation would have been shorter.
However, a real-time Renderman implementation is worthy goal.  It was
very convenient to make small chenges and watch them happen in real
time.