How I thought of the problem:
Very inefficiently. I thought about the bicubic
function in s and t underlying the bezier
control patch. Thus I evaluate a given bezier patch
at a given s and t:
function [res] = bez(C, MB, s, t)
%Test function to evaluate f(s,t)
on the bezier patch.
%The bezier magic matrix, the control
patch, and s and
%t are provided.
S = [s^3 s^2 s 1];
T = [t^3 t^2 t 1];
MIDDLE = MB*C*MB';
%This need only be computed once.
res(1) = S*MIDDLE*T';
%the coordinate value at (s,t).
Sd = [3*s^2 2*s 1 0];
res(2) = Sd*MIDDLE*T'; %the
derivative w/r to s, at (s,t).
Td = [3*t^2 2*t 1 0];
res(3) = S*MIDDLE*Td'; %the
derivative w/r to t, at (s,t).
I also compute the partials with respect to s and t at
the given point.
My function to actually draw the patches basically iterates
through all s's for a given
t and all t's for a given s, using the matlab line function
to add the resultant line seg-
ments to a 3d plot. (I have to call the above evaluation
function for x y and z for
all s and t.) The function is here.
(the input data is of the form here.)
I let matlab
handle all the interfacing, as in changing perspective
and aspect ratios. Also, the
length of the normal vectors I draw is fixed (at 3, actually),
which may not be ideal
for groups of bezier patches other than the teapot.
And I don't perform occlusion.
Here are some shots:
A close up on the lid and spout.
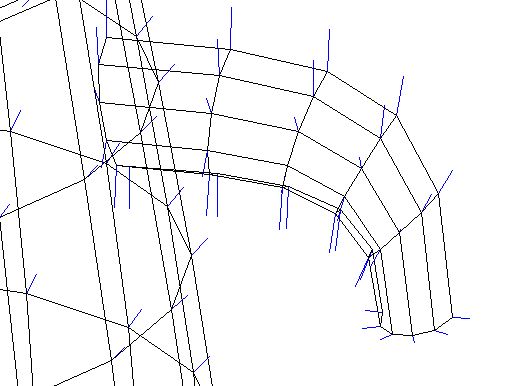
The quarter completed handle.
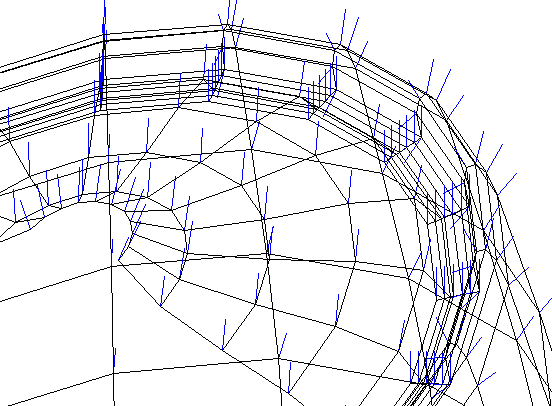
A close up on the lid. The concentration of vertices
here led me to allow multple resolutions.
Just for fun, a furry looking
teapot.
