The final exam will be cumulative. I will write a 1.5-hour exam that will be roughly 2/3 material we've covered since the last exam and 1/3 material covered in the first two exams. You will have two hours to complete the exam. The two hours will start at the beginning of the exam period. I am likely to give one question from a previous exam on the final, though it may vary slightly in the details,

The questions for the final exam covering the most recent material similar to (but not limited to) the questions below. You may want to study the previous exams and review questions for coverage of the earlier material.

1. Identify the following:
   • bottom-up dynamic programming
   • top-down dynamic programming
   • memoization
   • optimal substructure
   • longest common subsequence
   • graph
   • vertex
   • edge
   • subgraph
   • path
   • spanning tree
   • connected graph
   • undirected graph
   • directed graph
   • weighted graph
   • adjacency matrix
   • adjacency lists
   • minimum spanning tree
   • priority-first search (as in Dijkstra's and Prim's algorithms)
   • "label" or "representative" of an equivalence class (in Union-Find)
   • Union and Find operations


2. Write (pseudo-)code and state the running times for:
   • graph depth-first search using adjacency lists or an adjacency matrix
   • graph breadth-first search using adjacency lists or an adjacency matrix
   • Prim's minimum spanning tree algorithm for adjacency lists
   • Kruskal's minimum spanning tree algorithm for adjacency lists
   • Dijkstra's shortest path algorithm for adjacency lists


3. True/False. Explain your answer.
   • The running time of Prim's algorithm for a graph represented using adjacency lists is O(V lg V), where E is the number of edges and V is the number of vertices in a graph.
   • The number of edges in a minimum spanning tree of a weighted, connected graph is always one fewer than the number of vertices in the graph.
   • An edge-weighted graph has a unique minimum spanning tree if and only if its edge weights are distinct (i.e., no two edge weights are the same). If true explain why, if false give a counterexample.


4. What two properties are needed to make an optimization problem a good candidate for dynamic programming?


5. Give code or pseudocode for an efficient solution to the longest common subsequence problem (you should be able to do this for both the bottom-up and top-down approaches).


6. Give code or pseudocode for the rod-cutting problem (you should be able to do this for both the bottom-up and top-down approaches).


7. Give code or pseudocode for the Knapsack problem for the case of unlimited, indivisible objects (you should be able to do this for both the bottom-up and top-down approaches).



8. How can depth-first search be used to determine if a graph is connected?


9. What is the purpose of using the union-find data type in Kruskal's algorithm? Explain where in the algorithm it is used, what its inputs are, and what operations are applied.


10. What is the running time for depth-first search on a graph represented using an adjacency matrix? Using adjacency lists?


11. For the graph below, show the progess of Kruskal's, Prim's, and Dijkstra's algorithms. In particular, show the edges in order as they are added to the spanning or shortest-path tree. For Prim's and Dijkstra's algorithms, label each vertex with its weight and predecessor values after each new vertex is added to the minimum spanning tree/shortest-path tree.
    


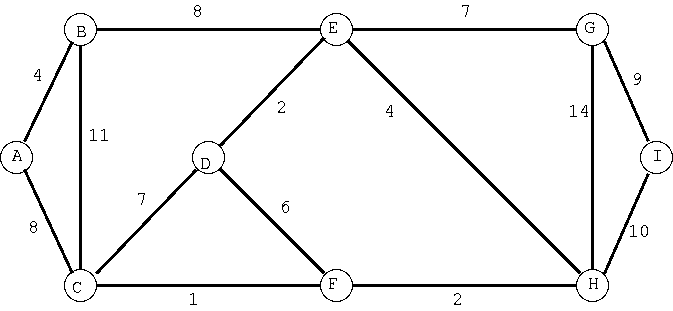
12. Computing single-source shortest distances in unweighted graphs (i.e., graphs where every edge represents the same distance) can be done with a simpler algorithm than Dijkstra's algorithm. In such graphs, distance is merely the number of edges on a path. Give such a simpler algorithm for finding single-source shortest paths in an unweighted graph.



13. Given a directed graph G on which each edge (u,v) has an associated value r(u, v), which is a real number in the range between from 0 to 1 that represents the reliability of a communication channel from u to v. We interpret r(u, v) as the probability that the channel from u to v will not fail, and we assume that these probabilities are independent. Modify Dijkstra's algorithm to find the most reliable path between two given vertices. [Note: this is a challenging question intended to get you thinking about other ways in which priority-first search can be used. It won't be on the exam, but figuring it out will improve your knowledge in ways that could help you on the exam.]