Bucknell Unversity Astronomy 101
All the Math You'll Need to Know

While this is not an aggressively mathematical course, mathematics is the language of science, and we can't talk about astronomy without using mathematical relationships. The good news here is that none of the mathematics you will see in this course should be new to you; it's all stuff that you encountered in high school. However, I realize that seeing it once in your distant past doesn't mean you remember it now, so this little page is a gentle reminder of some of the basic concepts.

Algebra

Solving Equations -- This is simply a question of moving around the terms in an equation until you get what you want on the left side and what it equals on the right side. If you can solve the following equation, then you can do Algebra. All you need to do here is divide both sides of the equation by 2, yielding, That's really all there is to it. Sometimes the equations are a bit more involved, but as long as you multiply, divide, add or subtract the same quantities on both sides of the equation, things should work out. So an equation like, You can play the same game with variables, so yields for m, What did I do here? I just multiplied both sides by R, divided both sides by G, and then divided both sides by m. Lastly, I switched the left side for the right side so that I ended up with an "m = " format.

Sometimes the quantity you're looking for is squared or cubed, i.e.,

Here we can use the same manipulations to get but then we need to take the square root of both sides to get the answer where "Sqrt()" means "take the square root of whatever's inside the parentheses." In each of these cases, the rule is always the same -- whatever you do to an equation, do it to both sides of the equation and the resulting equation will still be correct.

Geometry

Most of geometry is codified common sense. Here's an example:

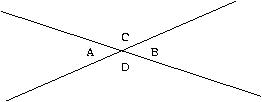
Where two straight lines cross, the "opposite angles" are equal. If you just stare at the figure for a minute, you'll realize that this has to be so. If it weren't true, one of the lines would have to be crooked. Therefore, A=B and C=D.

A variant on this is the old "line crossing a pair of parallel lines" rule:

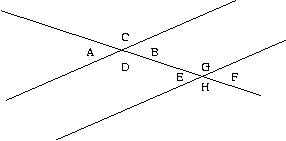
If the two lines running from lower left to upper right are parallel, then the line crossing these parallel lines must make the same angles with each one. Based on that logic, A=B=E=F, and C=D=G=H.

Right angles are special angles, and you should know that a right angle is a 90 degree angle.

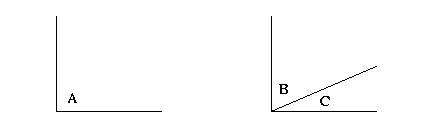
So in the figure above, A = 90. Moreover, if a right angle is broken into two angles as in right-hand panel in the figure above, these two angles must sum to 90 degrees, i.e., B + C = 90 degrees.

The same logic can be applied to a set of angles that span the "angle" made by a straight line.

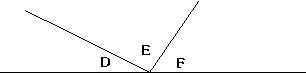
So, in the above diagram, D+E+F=180 degrees, or E+F= 180-D, or F = 180-D-E, or, well, you get the idea.

Trigonometry

I wish trig didn't have such a nasty-sounding name, because it's really not that complicated at all. It's nothing more than a few simple relationships between the angles and the lengths of the sides of a right triangle. A right triangle is a triangle with one right angle (since the sum of the angles in a triangle equals 180 degrees, there's no way to have more than on right angle in a triangle). Consider the right triangle below, where the right angle is at the left.

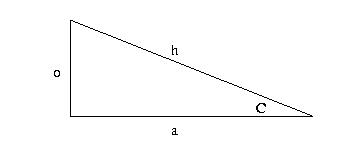
I've just picked one of the two non-right angles in the triangle and labeled it C. I've also labeled the lengths of each of the triangle's sides with lower case letters:
"o" for the side opposite the angle C,
"a" for the side adjacent to C, and
"h" for the "hypotenuse," which is the side opposite the right angle (it's also the longest side in the triangle).

The trig identities just relate the angle C to combinations of the lengths of the sides, so

You can find the sin(), cos(), and tan() functions on your calculator, and use them to determine the ratios between different lengths of the triangle. This is really useful because it provides a way to relate angles to lengths (for example, if you know the angle and one of the lengths, you can get the other length). We'll deal a lot with angles in this course ('cuz that's pretty much all we can really measure in astronomy), and trig will provide us with a way to figure out lengths and sizes of astronomical objects.

One last note -- be careful about the units of your angles. Most calculators have a switch that allows you to takes sin's and cos's of angles in either degrees units or radian units. For this course, it will be most useful if you stick to degree units, and therefore you should set your calculator to accept angles in degrees. Here's a way to test that your calculator is doing things right: calculate the sin of 90 degrees. It should be 1, but if you come up with some other number, your calculator is probably thinking you want the sin of 90 radians.

Scientific Notation

The numbers in astronomy or aften so huge that writing them out conventionally would take up way too much space (e.g., the distance from the Earth to the Sun is 150000000000 km). This is why astronomers use scientific notation to express these huge numbers more compactly. I won't write more about this here because your textbook (p. 541) does a pretty nice job with it. Please take a look at that description is you're uncomfortable interpreting numbers like Note that some calculators display this number as "1.7e+05" where the "e+05" means "105." Even if you're comfortable with this kind of notation, please make sure you can interpret your calculator's output before you need it on a problem set or exam.

Back to the Astronomy 101 Specials Page To the Astronomy 101 Home Page Questions and Comments?