ASTRONOMY 102 HOUR EXAM #1 PROBLEM ANSWERS

BUCKNELL UNIVERSITY

Astronomy 102

First Hour Exam

1999 February 19

Answers to Problems


Problem #1

For this problem, you'll need to apply the Observer's Triangle, which can be found on the front of your exam. The specific triangle we'll need to understand is diagramed below:

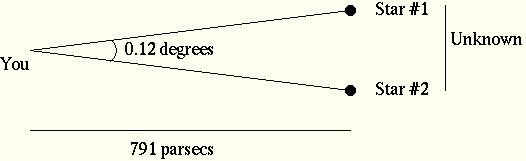
Note that the distance to the stars is indicated along the bottom, and the "unknown" distance between the two stars is the short side of this skinny triangle. If you stare at this triangle and the one on the front of your exam, you should be able to see by analogy that

Solving for the unknown distance, we get Note that the units come out as parsecs because the distance to the stars is expressed in parsecs and because the degree units cancel out in the ratio between 0.12 degrees and 57.3 degrees.

Return to Exam

Problem #2

OK, for this one, we'll need to remember how to get luminosities, and then how to do a ratio. Let's start with the luminosity. On the front of your exam, you find that

and also that as well as that Combining these three relations we get, Now, before we run off trying to calculate the luminosity of each star, let's look at the ratio of the luminosities: and where LG and LM are the luminosities of the G and M stars, respectively, and RG and RM are their radii. Consider the ratio: While at first, this looks incredibly messy, notice how much of it cancels out. The 5.67 x 10-8 W/(m2 K4) is on both top and bottom , as are the 4 x pi's. BVoth of those factors cancel out, leaving, and, since we're told that RG/RM = 10,

Return to Exam

Problem #3

This was a tricky problem because it involved a couple of separate steps. First, we need to figure out the frequency of the light emitted by the cloud. Then, we need to figure out how the frequency we measure on Earth is different from the emitted frequency because of the Doppler effect.

Let's start with the first part. On the front of your exam, you can find the following relation:

where h = 6.626 x 10-34 J s. We know the energy of the photons, and want to know their frequency, so let's solve for frequency: Now, the remainder of the problem is just a standard Doppler problem like the ones you dealt with in lab and in your homework. Look at the Doppler relation on the front of your exam: 
Doppler formula:                speed of emitter     change in frequency
                              ------------------- = --------------------
                                 speed of wave         rest frequency
In this problem, we know the rest frequency of the light (that's just the frequency the cloud thinks it's emitting, since the cloud isn't moving relative to itself), the speed of the emitter (200,000 m/s from the problem statement), and the speed of the wave (in this case, light, which moves at a speed of 3.0 x 108 m/s). So, we can solve for the change in frequency: Note that this is not the answer to the question, since it is the change in the frequency due to the Doppler effect, not the frequency observed. To figure out the observed frequency, we need to add or subtract the change to the rest frequency. Well, which one is it -- add or subtract? The cloud is coming toward us, so the waves are getting squished together, and therefore the number we measure per second will be higher than if there were no motion. Therefore, the frequency must be higher than the rest frequency, and we need to add the change in frequency to the rest frequency.