First Hour Exam |
1998 February 27 |
(Show your work!! I will be very generous with partial credit!!!)
Problem 1) A giant star of spectral type M0 has a luminosity 300 times larger than a typical Main Sequence M0 star. A Main Sequence M0 star has a radius of 1.0 x 108 m.
Part 1) What is the ratio of the intensities of the two stars?
Solution: For this part of the problem, the key piece of information is not a numerical value, such as the luminosity or the radius, but rather the spectral type of the two stars. Both stars have the same spectral type; since spectral type is a direct measurement of surface temperature, both stars must have the same surface temperature. Now, intensity can be calculated from the temperature as follows:
which was on the front of your exam. We can construct a ratio of the intensity of the giant to the intensity of the Main Sequence star as follows:
where IG and IMS are the intensities of the giant and Main Sequence stars, respectively. Since sigma is just a constant, we can cancel it out top and bottom, and get
But wait --- the temperatures are also the same, so the ratio of the intensities is just one; that is, both stars have the same intensity.
Part 2) What is the radius of the M0 giant?
Solution: Now we need some of that numerical data from the problem, but our life is a lot easier since we've already learned that the ratio of the intensities of the two stars is 1. Why? Because luminosity con be calculated from the following expression:
which appeared on the front of your exam. We don't actaully know the luminosities of either of the two stars, but we do know the luminosity ratio, so let's write down the luminosity ratio
where LG and LMS are the luminosities of the giant and Main Sequence stars, and SG and SMS are the surface areas of the giant and Main Sequence stars, respectively. We know from Part 1 above that IG and IMS are the same, so we can cancel out these quantities to get
The surface area of a star (which is a sphere), is
which appered on the front page of your exam. So,
where RG and RMS are the radii of the giant and Main Sequence stars, respectively. The 4 x pi's cancel out top and bottom, and we get
Now, we're told that LG/LMS = 300, and that RMS = 1.0 x 108 m, so the above becomes
so,
and then, taking the square root of both sides,
Problem 2) Sirius is a Main Sequence star with a surface temperature of 8000 K and a luminosity of 8.61 x 1027 W. It has a parallax of 1.053 x 10-4 degrees.
Part 1) Calculate its distance.
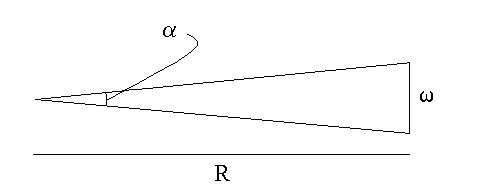
Solution: Nevermind about all of the temperature and luminosty stuff; the parallax alone is enough for us to calculate the distance to the star. Recall that the parallax is defined as the angle that a star appears to move relative to the background when the observer's vantage point changes by 1 Astronomical Unit. So, this problem is an application of the Observer's Triangle,

which appeared on the front of your exam. In this diagram, the star would be located at the apex of the triangle and the two vantage points would be at the endpoints of the seqment labelled w. Thus, w is 1 Astronomical Unit, or 1.495 x 1011 m, and alpha is the parallax angle, 1.053 x 10-4 degrees. R is the distance, which is what we're looking for, so
so
You may have chosen to calculate this number in units of Astronomical Units, in which case you answer would have been
Either answer (or the correct answer in pc, feet, or furlongs) is acceptable.
Part 2) Calculate the flux (in W/m2) from this star, when viewed from the Earth.
Solution: Now that we have the distance, all we need is the luminosity to calculate the flux, since
which can be found on the front of your exam. We're given the luminosity in the problem, so
Note that in order to get an answer in units of W/m2, you need to start with a luminosity in watts and a distance in meters.
Problem 3) Stars alpha gamma globulin and beta gamma globulin are members of an eclipsing spectroscopic binary system. Both stars have the same mass and orbit their common center of mass with velocity 3.0 x 105 m/s. An optical spectrum of the light from the binary system shows the following "w" shaped absorption line:
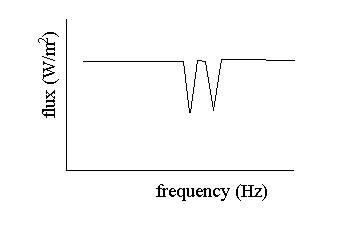
Part 1) Both absorption lines have been identified as due to the transition from the N=2 to N=3 energy levels of the hydrogen atom. The difference in energy between these two levels is 3.03 x 10-19 Joules. Calculate the rest frequency of the photons absorbed by this process.
Solution: Quite honestly, the hard part of this problem is the part you do before writing a single stroke on paper. There's a lot of information presented, and you need to sift through it to get to the important stuff.
For Part 1, you're asked to calculate the frequency of the photon absorbed by a hydrogen atom which makes a transition from the N=2 energy level to the N=3 energy level. You're told that the atom changed energy by 3.03 x 10-19 J when it absorbed the photon. Where did that energy come from? The photon! If that's so, then the energy of the photon is 3.03 x 10-19 J. Its energy and frequency are related by the following:
where h is Planck's constant, and this relation and the value of Planck's constant can be found on the front of your exam. So,
Part 2) Calculate the maximum frequency separation between the two absorption lines in the above spectrum due to the motions of the stars .
Solution: This is where the Doppler formula finally comes into play. In Part 1, we calculated the frequency of the absorption when viewed at rest with respect to the atom. However, because these two stars are orbiting around each other at a speed of 3.0 x 105, the absorption line from both stars will be shifted by the Doppler effect.
The stars are part of an eclipsing binary system, so we're seeing their orbits edge-on. Therefore, the maximum velocity difference along our line of sight will occur when one star is heading straight toward us and the other is heading straight away from us. (Draw a picture looking down on the system from above to see this clearly.)
By how much will each line be shifted? Well if one star is coming straight toward us, then the frequency shift of the absorption line can be calcualted from the Doppler formula
speed of emitter change in frequency
---------------------- = ----------------------
speed of wave rest frequency
where the speed of emitter is 3.0 x 105 m/s, the speed of the wave is the speed of light, 3.0 x 108 m/s, and the rest frequency is the frequency we calculated in Part 1 above. So,
This is the frequency shift of the absorption line for the star coming toward us. Because it is coming toward us, the frequency we detect is higher than the rest frequency by this amount. If you understand how we got this shift, then you should be able to see that the frequency shift of absorption line from the receding star will be the same, only for the receding star, the frequency we detect will be lower than the rest frequency by this amount. Thereofre, the frequency difference between the absorption line from the receding star and the absorption line from the approaching star will be twice the value found above, or